该现象在2000年之前十分知名……

阿凡提获得了1000斤萝卜，自身吃吃剩，要卖就需要去大市集。但由于阿凡提离群索居，住的区域很偏远。要去城内必须 穿越重生100里的荒漠蓝海。

已经知道阿凡提的毛驴较大载重量便是100斤，与此同时在荒漠里每走1里地，就必须 吞掉1斤萝卜。阿凡提必须 内置吃吃喝喝盘缠，因此不可以帮毛驴分摊重量。不言而喻，阿凡提没法一次性地把萝卜送到市集，可是他需要采用接下来的对策。

阿凡提事前带上毛驴把一部分萝卜掩埋在他沿线的隐秘地址，做为补充。自然，那样往返来回，也会耗费许多 萝卜。可是由于阿凡提亲自种的萝卜能够提升智商特性，因此每根价钱都等同于800年的老参——只需送至销售市场上，就算就一根盈利也非常大。

如今问，阿凡提一共能够在市集里售出多少斤萝卜？(留意要来回哦)

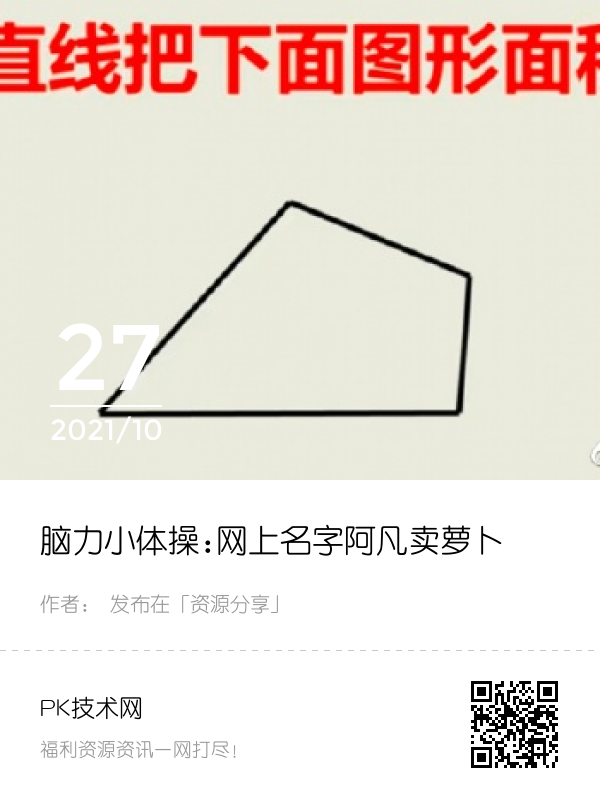
在网上广为流传的初中几何题目

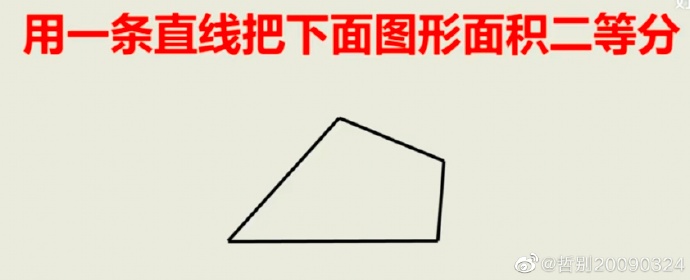
最先一点，觉得通过形心的平行线能够平分面积的念头是错的。

用 ID 为 ≠0 的表述

过形心等分的诸位，试一试等边三角形形心平行面于一边的平行线？形心是力的平衡，等同于每一个点以其到平行线的间距加了权，而算面积的是全部点的权均为 1。

例如，等边三角形，过几何中心且与一边平行面，则把初始三角形分为上边的小三角形和今天的梯状。小三角形和原三角形类似，相似比是2:3。则面积的比为4:9。显而易见，这根线沒有平分原图形的面积。

正确的答案

在四边形ABCD中，取对角BD的圆心O，联接OA，OC．显而易见，曲线段AO-OC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则平行线AE即是所愿。

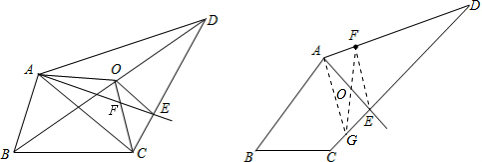
证实：

由于OE∥AC，
因此S△AOE=S△COE，
因此S△AOF=S△CEF，
又由于，曲线AOC能平分四边形ABCD的面积，
因此平行线AE平分四边形ABCD的面积

另一只鸡：

四边形ABCD。过AC圆心O做BD的直线，交AB或BC于P。平行线PD平分四边形ABCD。证实：因为O是AC圆心，不会太难发觉三角形AOB和三角形AOD面积占了四边形ABCD的一半。又因为OP平行面于BD，因此三角形OPD面积相当于三角形OPB的面积。四边形ABPD(或是三角形APD)面积相当于三角形AOB+三角形AOD-三角形OPB+三角形OPD，即四边形ABCD的一半。

翅痕

设顺时针方向四个端点为ABCD，联接在其中一个对角AC，过B点做AC的直线，那麼在这里条直线上随机挪动B点不容易转变三角形ABC的面积，将这一条直线与DC延伸线交叉与E，那麼就变成了平分三角形AED的难题，找到DE的定位点F，必须 F落在CD中间，联接AF即平分了面积。

此外，nerv同学们提及

这题要我想起以前上学的过程中想起的一个难题:针对随意茶叶蛋，是不是都存有一个方式 能一刀与此同时等分鸡蛋清和鸡蛋黄。每一次去买腊汁肉夹馍吃的过程中都是想一会，困惑了我很多年。

检索“三明治定律”，就能答疑解惑。